Inferensi Statistik
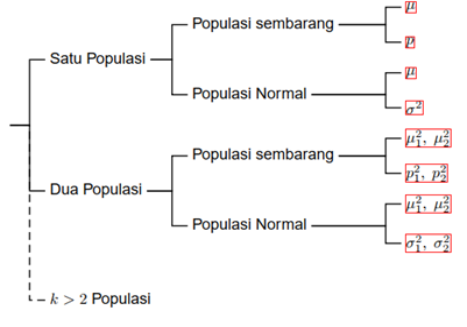
Inferensi statistik adalah pengambilan kesimpulan tentang parameter populasi berdasarkan analisis pada data sampel. Populasi adalah himpunan keseluruhan objek yang diamati sedangkan sampel merupakan himpunan bagian dari populasi. Selanjutnya yang dimaksud parameter adalah suatu karakteristik dari populasi. Konsep-konsep inferensi statistik meliputi estimasi titik, estimasi interval dan uji hipotesis.
Estimasi titik adalah menduga nilai tunggal parameter populasi. Sebagai contoh, parameter ![]() diduga dengan statistik
diduga dengan statistik ![]() , parameter
, parameter ![]() diduga dengan statistik
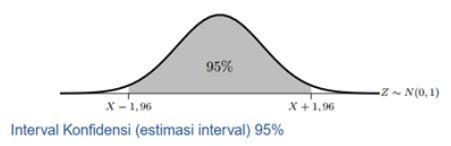
diduga dengan statistik ![]() . Sedangkan Estimasi interval yaitu menduga nilai parameter populasi dalam bentuk interval. Misalnya diduga dengan suatu interval
. Sedangkan Estimasi interval yaitu menduga nilai parameter populasi dalam bentuk interval. Misalnya diduga dengan suatu interval ![]() .
.
Uji rata-rata (mean) satu populasi digunakan untuk mengetahui bahwa mean dari populasi tersebut sama dengan harga tertentu (![]() ). Dalam kehidupan nyata tidak dimungkinkan untuk mengukur rata-rata (mean) dari seluruh populasi, untuk itu diambil sampal dari populasi tersebut yang kemudian dilakukan inferensi atau pengujian apakah nilai rata-rata yang dicurigai tersebut dapat diterima atau tidak berdasarkan informasi dari sampel yang telah diambil.
). Dalam kehidupan nyata tidak dimungkinkan untuk mengukur rata-rata (mean) dari seluruh populasi, untuk itu diambil sampal dari populasi tersebut yang kemudian dilakukan inferensi atau pengujian apakah nilai rata-rata yang dicurigai tersebut dapat diterima atau tidak berdasarkan informasi dari sampel yang telah diambil.
Uji hipotesis merupakan suatu proses untuk menentukan apakah dugaan tentang nilai parameter/karakteristik populasi didukung kuat oleh data sampel atau tidak. Ada dua jenis hipotesis yaitu hipotesis penelitian, dan hipotesis statistika. Hipotesis penelitian merupakan hipotesis tentang pernyataan dari hasil penelitian yang akan dilakukan, sedangkan hipotesis statistik suatu pernyataan tentang parameter populasi. ![]() adalah hipotesis yang akan diuji menggunakan suatu prosedur statistik, biasanya berupa suatu pernyataan tidak adanya perbedaan karakteristik populasi. Lawan dari hipotesis ini (
adalah hipotesis yang akan diuji menggunakan suatu prosedur statistik, biasanya berupa suatu pernyataan tidak adanya perbedaan karakteristik populasi. Lawan dari hipotesis ini (![]() ) adalah hipotesis alternative (
) adalah hipotesis alternative (![]() atau
atau ![]() ).
). ![]() digunakan untuk menunjukkan bahwa pernyataan mendapat dukungan kuat dari data.
digunakan untuk menunjukkan bahwa pernyataan mendapat dukungan kuat dari data. ![]() dianggap benar, kecuali data mendukung dengan kuat penolakan terhadap
dianggap benar, kecuali data mendukung dengan kuat penolakan terhadap ![]() .
.
Dalam pengujian suatu hipotesis sangat dimungkinkan terjadinya kesalahan dalam pengambilan kesimpulan. Kesalahan dalam menolak ![]() , padahal dalam kenyataannya
, padahal dalam kenyataannya ![]() tersebut benar dalam statistik dikenal dengan kesalahan tipe I atau biasa disimbolkan dengan
tersebut benar dalam statistik dikenal dengan kesalahan tipe I atau biasa disimbolkan dengan ![]() . Sedangkan peluang terkecil untuk menolak
. Sedangkan peluang terkecil untuk menolak ![]() yang salah biasa disebut dengan p-value. Dalam pengambilan keputusan dibutuhkan suatu daerah penolakan (daerah kritik), daerah penolakan ini merupakan himpunan (daerah) harga-harga dimana
yang salah biasa disebut dengan p-value. Dalam pengambilan keputusan dibutuhkan suatu daerah penolakan (daerah kritik), daerah penolakan ini merupakan himpunan (daerah) harga-harga dimana ![]() ditolak. Secara umum daerah penolakan pada uji hipotesis yaitu
ditolak. Secara umum daerah penolakan pada uji hipotesis yaitu ![]() ditolak (
ditolak (![]() diterima) jika nilai p-value <
diterima) jika nilai p-value < ![]() . Sebelum memutuskan apakah
. Sebelum memutuskan apakah ![]() ditolak atau tidak diperlukan statistik penguji. Statistik penguji tersebut merupakan suatu statistik atau variabel random yang digunakan untuk menentukan apakah
ditolak atau tidak diperlukan statistik penguji. Statistik penguji tersebut merupakan suatu statistik atau variabel random yang digunakan untuk menentukan apakah ![]() ditolak atau tidak ditolak. Bila statistik penguji masuk dalam daerah penolakan maka
ditolak atau tidak ditolak. Bila statistik penguji masuk dalam daerah penolakan maka ![]() ditolak, sebaliknya jika tidak maka
ditolak, sebaliknya jika tidak maka ![]() tidak ditolak.
tidak ditolak.
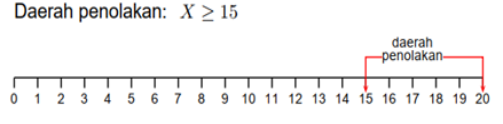
Secara umum, berikut langkah-langkah dalam uji hipotesis :
- Menentukan hipotesis
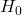 dan
dan 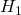
- Menentukan tingkat signifikansi (
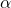 )
) - Menentukan dan hitung Statistik Penguji,
- Menentukan daerah kritik berdasarkan tingkat signifikansi
- Ambil kesimpulan berdasarkan
