Soal tentang Distribusi Binomial

Soal berikut merupakan soal tentang distribusi probabilitas, khususnya mengenai Distribusi Binomial.

Suatu survei menunjukkan bahwa hanya 70% dari mahasiswa yang disurvei tidak menyetujui pencalonan Ogah sebagai presiden mahasiswa. Bila kemudian diambil secara acak 12 mahasiswa, berapa peluang bahwa banyaknya yang tidak setuju Ogah menjadi presiden mahasiswa sebanyak

Tidak kurang dari 8 orang
Semuanya setuju

Jawab :

Soal tersebut dapat diselesaikan dengan menggunakan rumus fungsi kepadatan peluang distribusi Binomial.

Peluang tidak kurang dari 8 orang disini artinya lebih dari sama dengan 8 orang, sehingga 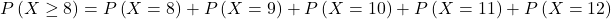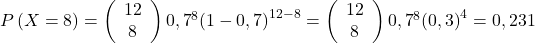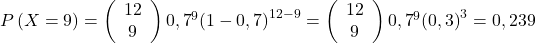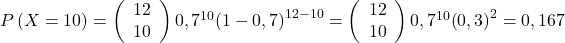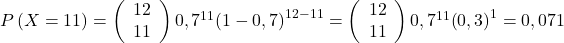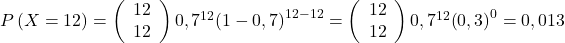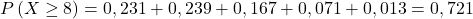$P\left(X\geq{}8\right)=P\left(X=8\right)+P\left(X=9\right)+P\left(X=10\right)+P\left(X=11\right)+P\left(X=12\right)$ , $P\left(X=8\right)=\left(\begin{array}{ cc}12 \\8\end{array}\right){0,7}^8{\left(1-0,7\right)}^{12-8}=\left(\begin{array}{cc}12 \\8\end{array}\right){0,7}^8{\left(0,3\right)}^4=0,231$ , $P\left(X=9\right)=\left(\begin{array}{ cc} 12 \\ 9 \end{array}\right){0,7}^9{\left(1-0,7\right)}^{12-9}=\left(\begin{array}{ cc} 12 \\ 9 \end{array}\right){0,7}^9{\left(0,3\right)}^3=0,239$ , $P\left(X=10\right)=\left(\begin{array}{ cc} 12 \\ 10 \end{array}\right){0,7}^{10}{\left(1-0,7\right)}^{12-10}=\left(\begin{array}{ cc} 12 \\ 10 \end{array}\right){0,7}^{10}{\left(0,3\right)}^2=0,167$ , $P\left(X=11\right)=\left(\begin{array}{ cc} 12 \\ 11 \end{array}\right){0,7}^{11}{\left(1-0,7\right)}^{12-11}=\left(\begin{array}{ cc} 12 \\ 11 \end{array}\right){0,7}^{11}{\left(0,3\right)}^1=0,071$ , $P\left(X=12\right)=\left(\begin{array}{ cc} 12 \\ 12 \end{array}\right){0,7}^{12}{\left(1-0,7\right)}^{12-12}=\left(\begin{array}{ cc} 12 \\ 12 \end{array}\right){0,7}^{12}{\left(0,3\right)}^0=0,013$ , $P\left(X\geq{}8\right)=0,231+0,239+0,167+0,071+0,013=0,721$ . Sehingga peluang banyaknya yang tidak setuju Ogah menjadi presiden mahasiswa sebanyak tidak kurang dari 8 orang adalah 0,721.

Peluang semuanya setuju dapat juga diartikan bahwa tidak ada yang tidak setuju, sehingga $P\left(X=0\right)=\left(\begin{array}{cc}12 \0\end{array}\right){0,7}^{0}{\left(1-0,7\right)}^{12-0}=\left(\begin{array}{cc}12 \\0\end{array}\right){0,7}^{0}{\left(0,3\right)}^{12} = 0,0000005314$ .

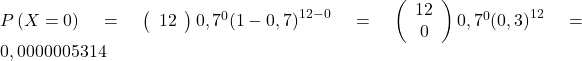Sehingga peluang semuanya setuju Ogah menjadi presiden mahasiswa adalah 0,0000005314.

Soal tentang Distribusi Binomial

Submit a Comment Cancel reply