[et_pb_section fb_built=”1″ custom_padding_last_edited=”on|phone” admin_label=”Header” _builder_version=”3.22″ use_background_color_gradient=”on” background_color_gradient_start=”rgba(60,190,190,0.2)” background_color_gradient_end=”rgba(255,255,255,0.98)” background_color_gradient_overlays_image=”on” background_image=”http://zaib.sandbox.etdevs.com/divi/wp-content/uploads/sites/2/2018/07/language-school-illustration-13.png” background_position=”bottom_center” custom_padding=”0px||0px||true|false” custom_padding_tablet=”140px|0px|50px|0px|false|false” custom_padding_phone=”120px|||”][et_pb_row _builder_version=”3.25″ background_size=”initial” background_position=”top_left” background_repeat=”repeat” max_width=”1280px” use_custom_width=”on” custom_width_px=”1280px”][et_pb_column type=”4_4″ _builder_version=”3.25″ custom_padding=”|||” custom_padding__hover=”|||”][et_pb_text _builder_version=”4.4.2″ text_font=”||||||||” text_font_size=”18px” text_line_height=”2em” header_font=”EB Garamond||||||||” header_font_size=”60px” header_line_height=”1.3em” text_orientation=”center” max_width=”938px” module_alignment=”center” custom_margin=”|85px||||” custom_padding=”||0px|||” text_font_size_tablet=”” text_font_size_phone=”15px” text_font_size_last_edited=”on|phone” text_line_height_tablet=”” text_line_height_phone=”1.6em” text_line_height_last_edited=”on|phone” header_font_size_tablet=”50px” header_font_size_phone=”32px” header_font_size_last_edited=”on|phone”]

Abraham De Moivre :

Penemu Distribusi Normal sebagai Pendekatan Distribusi Binomial

[/et_pb_text][/et_pb_column][/et_pb_row][/et_pb_section][et_pb_section fb_built=”1″ _builder_version=”4.4.2″ custom_padding=”3px|||||”][et_pb_row column_structure=”2_5,3_5″ _builder_version=”4.4.2″][et_pb_column type=”2_5″ _builder_version=”4.4.2″][et_pb_image src=”https://metstat.mipa.ugm.ac.id/wp-content/uploads/sites/1298/2020/10/Abraham-de-moivre.png” _builder_version=”4.4.2″ custom_padding=”||0px|4px||”][/et_pb_image][/et_pb_column][et_pb_column type=”3_5″ _builder_version=”4.4.2″][et_pb_text _builder_version=”4.4.2″ custom_padding=”6px|||||”]

Abraham De Moivre kecil lahir pada tanggal 26 Mei 1667 di Champagne, Perancis. Ayahnya adalah seorang yang sangat mencintai pendidikan. Hal inilah yang mendorong De Moivre kecil untuk mendapatkan pendidikan yang baik. Pendidikan formal pertamanya dimulai ketika pindah ke Paris dan mengambil kelas privat dari Jacques Ozanam pada tahun 1684. Namun, pada masa awal penindasan agama di Perancis, keluarga De Moivre’s pindah ke London.

Ketika berada di London itulah Abraham De Moivre mulai menguasai matematika dan dalam waktu singkat menjadi ahli matematika. Dia membaca buku karangan Newton berjudul ‘Principia’ dan mulai menyadari bahwa ada banyak hal untuk dipelajari. Dengan cepat dia menguasai isi tulisan Newton tersebut. Bahkan, Newton sendiri mengakuinya dengan mengatakan ”pergilah kepada Tuan De Moivre; dia jauh lebih tahu tentang hal ini daripada aku”. Ini merupakan penghormatan yang luar biasa.

[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row column_structure=”3_5,2_5″ _builder_version=”4.4.2″][et_pb_column type=”3_5″ _builder_version=”4.4.2″][et_pb_text _builder_version=”4.4.2″]

[/et_pb_text][/et_pb_column][et_pb_column type=”2_5″ _builder_version=”4.4.2″][et_pb_image src=”https://metstat.mipa.ugm.ac.id/wp-content/uploads/sites/1298/2020/10/kurva-binomial-normal.png” _builder_version=”4.4.2″ custom_margin=”||-4px|||” custom_padding=”21px|||32px||”][/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row _builder_version=”3.25″ background_size=”initial” background_position=”top_left” background_repeat=”repeat”][et_pb_column type=”4_4″ _builder_version=”3.25″ custom_padding=”|||” custom_padding__hover=”|||”][et_pb_text _builder_version=”3.27.4″ background_size=”initial” background_position=”top_left” background_repeat=”repeat”]

Distribusi Binomial

Distribusi binomial merupakan salah satu distribusi peluang untuk variabel random diskit. Eksperimen/percobaan memenuhi distribusi binomial apabila dilakukan dengan pengembalian sebanyak $n$ kali dengan $x$ kali sukses. Dalam setiap eksperimennya hanya ada dua kemungkinan yaitu, sukses dengan peluang sebesar $p$ dan gagal dengan peluang sebesar $q$ . Antar eksperimen bersifat independen.
Fungsi kepadatan peluang variabel random diskrit (probability mass function / pmf) X dengan $x$ kali sukses dalam $n$ kali eksperimen dinyatakan dengan
$f(x;n,p)=\bigl(\begin{smallmatrix} n\\ x \end{smallmatrix}\bigr)p^{x}q^{n-x}, \: x=0,1,2,...,n$ dengan
$(\begin{smallmatrix} n\\ x \end{smallmatrix}\bigr)=\frac{n!}{x!(n-x)!}$

Distribusi Normal

Distribusi normal adalah salah satu distribusi peluang untuk variabel random kontinu. Distribusi normal merupakan distribusi probabilitas yang paling banyak digunakan dalam berbagai analisis statistika, baik pada ilmu alam, maupun pada ilmu sosial. Distribusi ini memiliki kurva lonceng (bell curve) untuk menggambarkan fungsi kepadatan peluangnya. 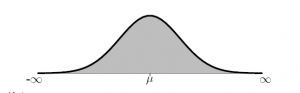Empat sifat kurva normal yaitu, simetris terhadap sumbu vertikal $\mu$ (mean); memotong sumbu mendatar ( $x$ ) secara asimtotis; nilai modus dan median terletak pada $x=\mu$ (nilai modus dan median sama dengan nilai mean); dan luas daerah dibawah kurva normal adalah 1. 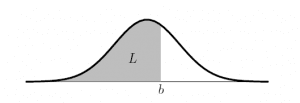Peluang kumulatif kurang dari suatu nilai $x=b$ atau $P(X)\leq b$ ditunjukkan oleh luas daerah di kiri $x=b$ pada kurva normal.
Fungsi kepadatan peluang variabel random kontinu (probability density function/pdf) normal dengan mean = $\mu$ dan variansi = $\sigma ^{2}$ adalah
$f(x;\mu ,\sigma ^{2})=\frac{1}{\sqrt{2\pi \sigma ^{2}}}e^{\frac{-(x-\mu )^{2}}{2\sigma ^{2}}},\: -\infty < x< \infty$
dengan
$-\infty < \mu < \infty$ dan $\sigma ^{2} \geq 0$

Distribusi normal sebagai pendekatan distribusi binomial

Nilai-nilai peluang untuk eksperimen/percobaan binomial dapat diperoleh dengan rumus fungsi kepadatan peluang untuk distribusi binomial, tetapi untuk $n$ cukup besar, maka nilai peluang tersebut dapat dicari dengan pendekatan distribusi normal dimana $\mu =np$ dan $\sigma ^{2}=npq$ . Namun, karena variabel random binomial merupakan variabel random diskrit sedangkan distribusi normal merupakan variabel random kontinu, maka
$P(X=b)=P(b-0,5< X\leq b+0,5)=\int_{b-0,5}^{b+0,5}\frac{1}{\sqrt{2\pi \sigma ^{2}}}e^{\frac{-(x-\mu )^{2}}{2\sigma ^{2}}}dx.$

[/et_pb_text][/et_pb_column][/et_pb_row][/et_pb_section]

Abraham De Moivre : Penemu Distribusi Normal sebagai Pendekatan Distribusi Binomial

Abraham De Moivre :

Penemu Distribusi Normal sebagai Pendekatan Distribusi Binomial

Leave A Comment Cancel reply