Peluang

Peluang atau disebut juga probabilitas merupakan harga angka yang menunjukkan seberapa besar kemungkinan suatu peristiwa atau kejadian akan terjadi. Nilai peluang di antara 0 dan 1. Peluang kejadian 0 artinya kejadian tersebut tidak mungkin terjadi. Sedangkan peluang kejadian 1 artinya kejadian tersebut pasti terjadi.

Ada 3 hal yang harus diketahui untuk mendapatkan nilai peluang suatu kejadian yaitu, eksperimen, ruang sampel, dan kejadian.

Eksperimen merupakan percobaan yang memiliki variasi dalam hasilnya. Ruang sampel merupakan himpunan semua hasil yang mungkin dari suatu eksperimen. Ruang sampel sering dinotasikan dengan Ω atau $S$ . Sedangkan kejadian merupakan himpunan bagian dari ruang sampel dan biasa dinotasikan dengan huruf kapital. Misalkan suatu eksperimen melemparkan dadu setimbang sebanyak satu kali, apabila hasil yang mungkin adalah munculnya angka, maka ruang sampel, $S=\left \{ 1, 2, 3, 4, 5, 6 \right \}$ , dan kejadian munculnya angka genap $A=\left \{ 2, 4, 6 \right \}$ .

Suatu kejadian baru dapat terbentuk dari satu kejadian atau dua kejadian yang lain.

Komplemen suatu kejadian $A$ yang dinotasikan dengan $A^{c}$ merupakan himpunan bagian dari $S$ tetapi bukan anggota $A$ atau $A^{c}=\left \{ x\in S, x\notin A \right \}.$
Gabungan kejadian $A$ dan kejadian $B$ , dinotasikan dengan $A\cup B$ yaitu, himpunan bagian dari $S$ dan anggotanya merupakan anggota kejadian $A$ atau kejadian $B$ atau $A\cup B=\left \{ x\in S, x\in A\: atau\: x\in B \right \}.$
Irisan kejadian $A$ dan kejadian $B$ , dinotasikan dengan $A\cap B$ yaitu, himpunan bagian dari $S$ dan anggotanya merupakan anggota kejadian $A$ dan $B$ , atau $A\cap B =\left \{ x\in S, x\in A\: dan\: x\in B \right \}.$

Jika diketahui jumlah anggota ruang sampel $S$ yaitu $n(S)$ dan jumlah anggota kejadian $A$ yaitu $n(A)$ , maka nilai peluang terjadinya kejadian $A$ adalah
$P(A)=\frac{n(A)}{n(S)}$
dengan

$P(A)\geqslant 0$
$P(S)=1$
Jika $A$ dan $B$ independen, maka $P(A\cup B)=P(A)+P(B)$

Kejadian Saling Asing (Mutually Exclusive)

Kejadian saling asing adalah kejadian-kejadian yang tidak mungkin terjadi secara bersamaan atau untuk dua kejadian $A$ dan $B$ , $A\cap B=\varnothing$ , sehingga berlaku

$P(A\cup B)=P(A)+P(B)-P(A\cap B)=P(A)+P(B)$

Peluang Bersyarat (Conditional Probability)

Ada kalanya suatu kejadian akan dipengaruhi oleh kejadian lainnya. Peluang suatu kejadian jika diketahui suatu kejadian lainnya disebut dengan peluang bersyarat. Peluang kejadian $A$ jika diketahui peluang kejadian $B$ dinyatakan dengan

$P(A|B)=\frac{P(A\cap B)}{P(B)}$

dengan syarat $P(B)\neq 0$ .

Kejadian Saling Independen

Kejadian saling independen adalah kejadian-kejadian yang tidak saling mempengaruhi. Dua kejadian dikatakan saling independen apabila
$P(A\cap B)=P(A)P(B).$

Peluang Total (Total Probability) dan persamaan Bayes

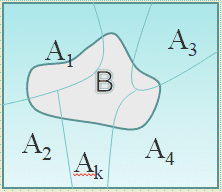Misalkan $A_{1}, A_{2}, ... , A_{k}$ adalah semua partisi dari ruang sampel $S$ yang saling asing dengan $P(A_{i})> 0,\: i=0, 1,2,...k$ , maka untuk setiap $B\subseteq S$ , peluang total $B$ yaitu
$P(B)=\sum_{i=1}^{k}P(A_{i}\cap B)=\sum_{i=1}^{k}P(A_{i})P(B|A_{i})$
dan persamaan bayes yaitu
$P(A_{i}|B)=\frac{P(A_{i})P(B|A_{i})}{\sum_{i=1}^{k}P(A_{i})P(B|A_{i})}$

Red. Yunita, 2020

Peluang

Submit a Comment Cancel reply